Las resistencias eléctricas tienen unas bandas de colores que te permiten conocer su valor en ohmios y otra información importante. Es el código de colores de las resistencias.
Puedes encontrar resistencias con 4, 5 y hasta 6 bandas. Estas bandas pueden representar un dígito, el multiplicador, la tolerancia o el coeficiente de temperatura.
Los colores tienen los mismos valores independientemente del número de bandas, pero tendrás que interpretarlos de diferente manera. En los siguientes puntos veremos cómo calcular los valores de las resistencias dependiente de los colores de sus bandas.
Código de colores de las resistencias
En la siguiente tabla puedes consultar los valores que tienen los colores de las resistencias:
| Color | Dígitos | Multiplicador | Tolerancia | Coeficiente de temperatura |
|---|---|---|---|---|
| Negro | 0 | 1 (10^0) | ||
| Marrón | 1 | 10 (10^1) | +-1% | 100 ppm |
| Rojo | 2 | 100 (10^2) | +-2% | 50 ppm |
| Naranja | 3 | 1000 (10^3) | 15 ppm | |
| Amarillo | 4 | 10000 (10^4) | 25 ppm | |
| Verde | 5 | 100000 (10^5) | +-0.5% | |
| Azul | 6 | 1000000 (10^6) | +-0.25% | |
| Violeta | 7 | 10000000 (10^7) | +-0.1% | |
| Gris | 8 | |||
| Blanco | 9 | |||
| Plateado | 0.01 | +-10% | ||
| Dorado | 0.1 | +-5% |
Una banda puede representar un dígito, el multiplicador, la tolerancia o el coeficiente de temperatura. Depende de la posición que ocupe y del tipo de resistencia (4, 5 o 6 bandas).
En los siguientes puntos veremos cada uno de estos elementos en detalle y cómo interpretar los colores en función del tipo de resistencia.
Resistencias de 4 bandas
Vamos a comenzar por las resistencias de 4 bandas. Como su nombre indica, tienen pintadas 4 bandas de diferentes colores.
Las dos primeras bandas son dígitos, la tercera es el multiplicador y la cuarta es la tolerancia.
Supongamos que tenemos esta resistencia:
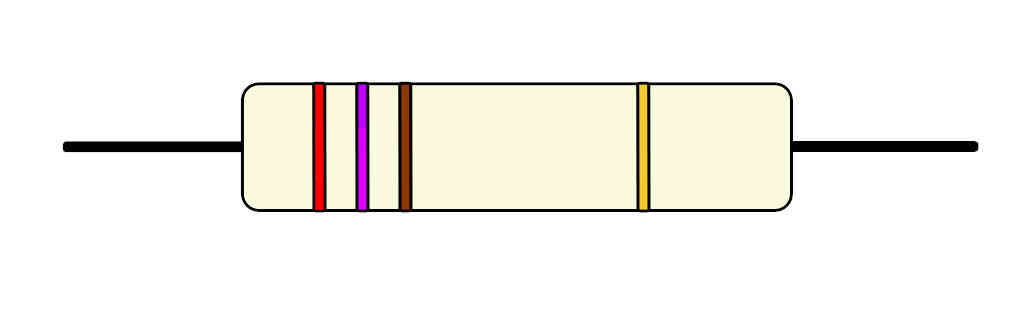
La primera banda es roja. Si miramos en la tabla de colores de resistencias, el rojo en la columna de dígitos tiene valor 2.
La segunda banda es violeta, y en la tabla tiene valor 7.
Al tratarse de dígitos van consecutivos. En este caso tendríamos un 27.
Ahora vamos con la tercera banda, que es el multiplicador y es de color marrón. En la tabla, en la columna del multiplicador, el marrón tiene valor 10.
Una vez obtenidos estos valores tenemos que multiplicar el 10 por el 27 de los dígitos. El resultado es el valor de la resistencia en ohmios. En este caso 27 * 10 = 270 ohm.
Y por último, la cuarta banda es la tolerancia. Nos indica cuanto (en porcentaje) puede variar el valor indicado de la resistencia. En este caso la banda es dorada. Según la tabla tendría una tolerancia de +-5%, es decir, toleraría un valor que superase hasta en un 5% los 270ohm que hemos calculado antes. También soportaría valores que estuviesen un 5% por debajo del calculado. La tolerancia es importante puesto que los valores de las resistencias están normalizados y no existen resistencias de todos los valores.
Al final de la página tienes una tabla con los valores normalizados de las resistencias.
Resistencias de 5 bandas
Vamos a seguir con las resistencias de 5 bandas.
Las tres primeras bandas son dígitos, la cuarta es el multiplicador y la quinta es la tolerancia.
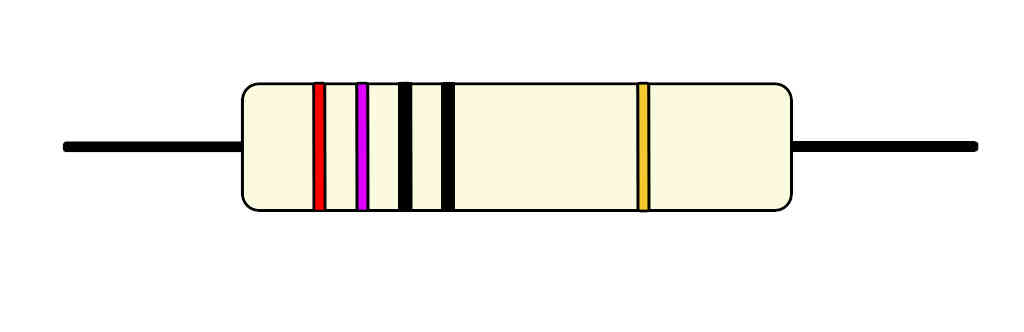
El procedimiento a seguir es similar al de 4 bandas. La única diferencia es que hay un dígito más.
Vamos a analizar la resistencia de la imagen:
Las dos primeras bandas son iguales que las del ejemplo de 4 bandas del punto anterior. La primera banda es roja y tiene valor 2 en la columna dígitos de la tabla. La segunda banda es violeta y tiene valor 7.
La diferencia con la resistencia de 4 bandas es que, en este caso, la tercera banda también es un dígito. En la resistencia de la imagen la tercera banda es negra y el valor que tiene en la tabla, en la columna de los dígitos, es el 0.
Tomando estos tres valores consecutivos obtenemos el 270.
En las resistencias de 5 bandas, el multiplicador es la cuarta banda. En este ejemplo es de color negro. Si miras la tabla, el negro en la columna del multiplicador tiene valor 1. Así que multiplicamos el 270 de los dígitos por el 1 del multiplicador. El resultado es 270 * 1 = 270ohm.
Ya solo nos queda la tolerancia, que es la quinta banda. Como en el caso anterior, también es dorada, por lo que la tolerancia es de +-5% (consulta la tabla). Por lo tanto, esta resistencia soportará valores un 5% por encima y por debajo de los 270ohms.
Resistencias de 6 bandas
Hemos llegado al último tipo de resistencia, las de 6 bandas.
Son exactamente iguales que las de 5 bandas con la diferencia de que incluyen una sexta banda que representa el coeficiente de temperatura.
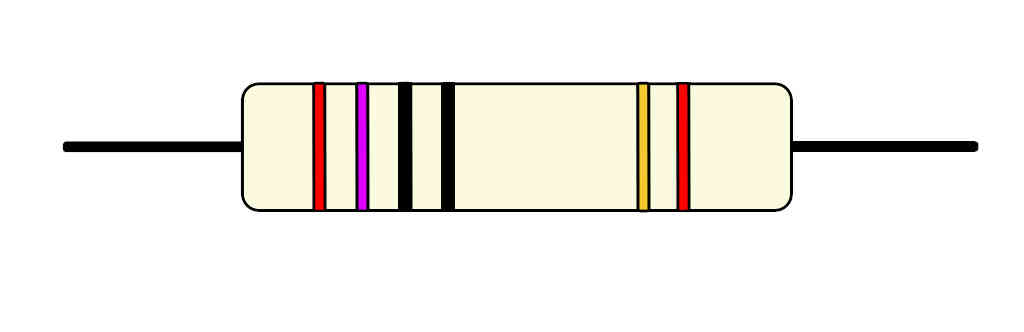
Este coeficiente indica cómo aumenta o disminuye la resistencia con la variación de la temperatura. Es un concepto un poco complicado de explicar así que intentaré plantearlo de la forma más sencilla y clara posible (no quiero dar una explicación técnica, solo que lo entiendas).
El coeficiente de temperatura se mide en ppm (partes por millón). Esto significa que si la resistencia tiene, por ejemplo, un coeficiente de temperatura de 50ppm, el valor de la resistencia variaría 0.00005 (50/1000000) ohmios por cada grado que varía la temperatura nominal de esta.
Para saber el coeficiente de temperatura de la resistencia consulta el color de la sexta banda en la última columna de la tabla que vimos al principio. Para este ejemplo, el coeficiente de temperatura 50ppm corresponde al color rojo.
Vamos a ver un ejemplo para que quede más claro. Supongamos que la resistencia tiene una temperatura nominal de 25ºC. Si la temperatura de trabajo es de 30ºC y trabajamos con una resistencia con un coeficiente de temperatura de 50ppm, el valor de esta variaría 0.00025 ohmios, puesto que trabajamos con 5ºC por encima de la temperatura nominal de la resistencia. Como vimos anteriormente, con un coeficiente de temperatura 50ppm, la resistencia varía 0.00005 ohmios por cada grado de diferencia. Al variar 5ºC, el cálculo es el siguiente: 5 * 0.00005 = 0.00025 ohmios.
Valores normalizados de las resistencias
En la siguiente tabla puedes consultar los valores normalizados de las resistencias. Como puedes comprobar existen las resistencias de 270ohm que calculamos en los apartados anteriores:
| x10 | x100 | x1000 | x10000 | x100000 | x1000000 | |
| 1 Ω | 10 Ω | 100 Ω | 1K Ω | 10k Ω | 100K Ω | 1M Ω |
|---|---|---|---|---|---|---|
| 1.2 Ω | 12 Ω | 120 Ω | 1K2 Ω | 12K Ω | 120K Ω | 1M2 Ω |
| 1.5 Ω | 15 Ω | 150 Ω | 1K5 Ω | 15K Ω | 150K Ω | 1M5 Ω |
| 1.8 Ω | 18 Ω | 180 Ω | 1K8 Ω | 18K Ω | 180K Ω | 1M8 Ω |
| 2.2 Ω | 22 Ω | 220 Ω | 2K2 Ω | 22K Ω | 220K Ω | 2M2 Ω |
| 2.7 Ω | 27 Ω | 270 Ω | 2K7 Ω | 27K Ω | 270K Ω | 2M7 Ω |
| 3.3 Ω | 33 Ω | 330 Ω | 3K3 Ω | 33K Ω | 330K Ω | 3M3 Ω |
| 3.9 Ω | 39 Ω | 390 Ω | 3K9 Ω | 39K Ω | 390K Ω | 3M9 Ω |
| 4.7 Ω | 47 Ω | 470 Ω | 4K7 Ω | 47K Ω | 470K Ω | 4M7 Ω |
| 5.1 Ω | 51 Ω | 510 Ω | 5K1 Ω | 51K Ω | 510K Ω | 5M1 Ω |
| 5.6 Ω | 56 Ω | 560 Ω | 5K6 Ω | 56K Ω | 560K Ω | 5M6 Ω |
| 6.8 Ω | 68 Ω | 680 Ω | 6K8 Ω | 68K Ω | 680K Ω | 6M8 Ω |
| 8.2 Ω | 82 Ω | 820 Ω | 8K2 Ω | 82K Ω | 820K Ω | 8M2 Ω |
| 10M Ω |
Conocer el margen de tolerancia te será muy útil para encontrar la resistencia más aproximada en caso de no existir una con el valor exacto.
Siempre que calcules una resistencia aplicando la Ley de Ohm, debes consultar esta tabla para saber si existe el valor que has obtenido o si debes elegir otro aproximado teniendo en cuenta el margen de tolerancia.
¡Suscríbete a la newsletter y no te pierdas nada!
Te avisaré cuando publique nuevo contenido en paraarduino.com y en mi canal de YouTube (@ParaArduino).
